ハッピー・ノート.com

前回に引き続き、今回は「短時間に膨大な問題をさばく能力」についてです。

今回お話しする処理能力は、志望校によって必要か不必要かがわかれます。やや番外編的ですので、志望校が中堅校未満の場合はあまり必要ありません。

この代表例が今回は筑波大学附属中学（以下筑附）です。

一般的に、中学入試は50分ないし60分で大問が5題程度出題されます。

しかし、筑附は「社会と合わせて50分」「算数大問10題、社会大問7題」とあまりに桁外れです。

しかも、問1は小問が7つもあり、これらの小問は１つあたり25秒で解かねばなりません。

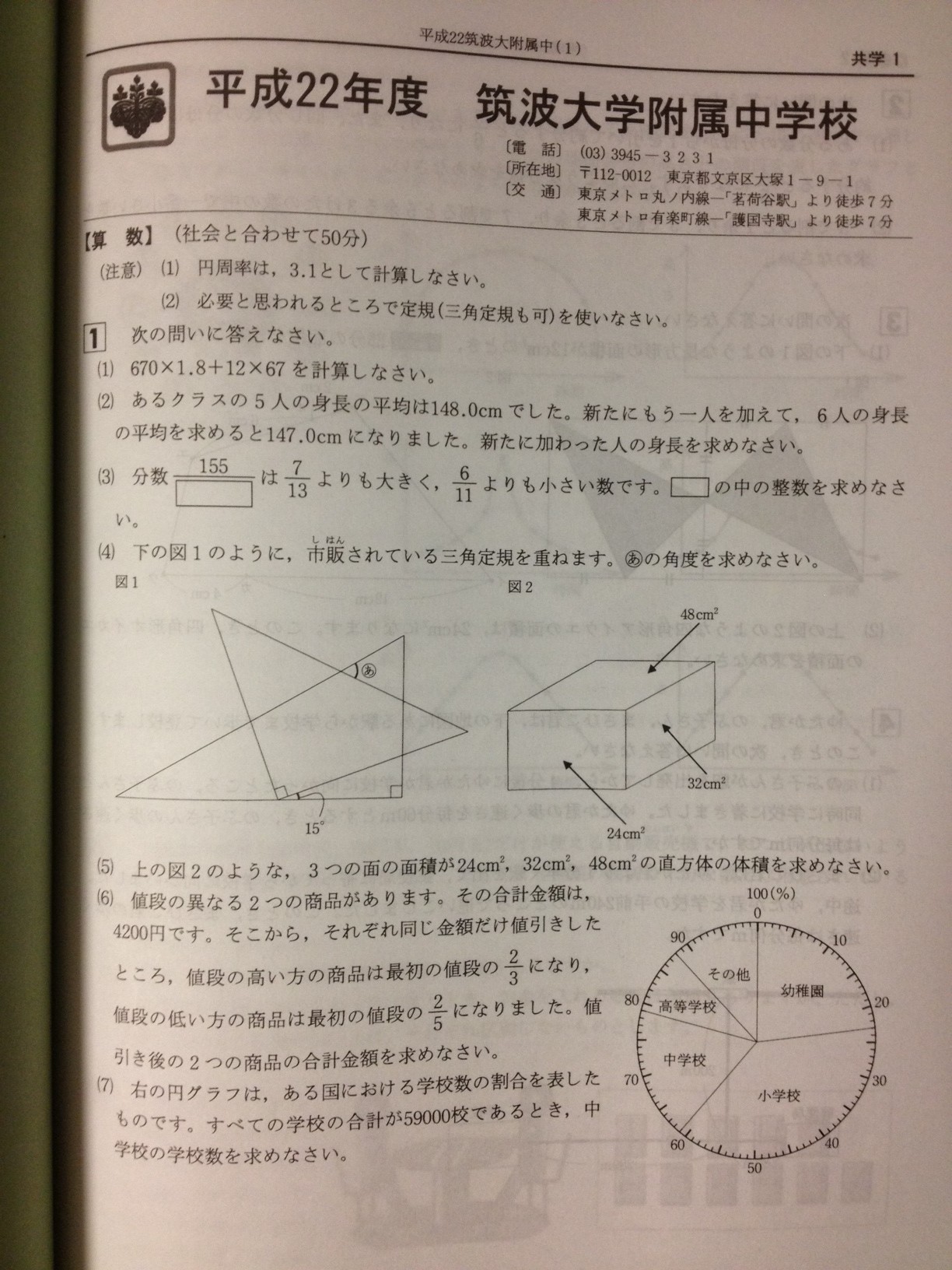
Ｈ22　筑波大学附属中学

（出典：声の教育社）

このタイプの学校は、解く時に「一瞬でも悩んだらアウト」です。

では、どのように訓練すれば良いのでしょうか。

短時間に膨大な問題を課してくる学校は、基本～応用止まりの問題で入試を構成します（これは高校入試、大学入試にも通じます）。

つまり、難問奇問に取り組む必要はなく、「基本→応用」という、ごく一般的なプロセスをきちんと踏むことが大切です。

ただし、瞬時に

「約数問題の“あまり一定”パターンだな」

「これは速さを装っているけれど、実際はつるかめ算だな」

「場合の数の中でも、書き出ししか方法がないな」

と、問題タイプを判断する必要があります。そのためには

１．それぞれの単元内で、さらに自分なりに細分化した引き出しを持つこと

２．とにかく数多くの問題にあたり、１の引き出しを一発で探り当てる訓練をする

３．１，２を基本問題、応用問題に対して繰り返す

練習をします。

今日はパーティーだから散らし寿司にしよう

↓

ご飯はかために炊かないとね

↓

今日は新米しかない

↓

普段のシャリより、さらに水を少な目にしなければ

という発想が瞬時にできるかどうか。

頭の中で「大皿料理」「炭水化物」「ご飯の炊き方」「新米の特性」など、様々な事柄がきちんと分類されていないと、「雑炊か散らし寿司か」が判断し、「シャリは水分少な目」というパターンがわかっており、「新米は古米より水分含有量が多い」という基本と理由がわかっていないとできませんよね。

もちろん、参考書や塾のカリキュラムは算数を分類しています。しかしそれは大局的なものであり、細分化まではされていません。人によってその分類が「わかりやすい」「わかりにくい」というのも変わってきます。

そこで、自分にとって最もわかりやすい分類、つまり「引き出し」を作る事が必要です。

そして、その引き出しを作って確固たるものにするには、相当数の演習を積んで算数全体を俯瞰できる「余裕」。前回に引き続いて言うなら、仕事算を5パターンだけでなく10パターンほど解いておく位の余裕は必要です。そのためにも応用問題レベル（発展はいりません）までスキルを磨きましょう。